Students often view mathematics as merely a collection of formulas they have to memorize, rather than ideas they need to understand. Because of this, students learning mathematics can miss some of the important connections between ideas within mathematics.
Missing the connections between ideas makes mathematics both less interesting and more difficult to learn. It is less interesting because it removes the connections between the ideas. It is more difficult because when you remove the links between ideas, they are harder to memorize. For instance, it is easier to remember your division facts when you realize that division is just the reverse of multiplication. Then, you only really have to memorize your multiplication facts to learn both multiplication and division.
The Struggle of Understanding the Distance Formula
One place where I see students needlessly struggling is in understanding the distance formula. The distance formula tells you how to measure the distance between two points in a Cartesian coordinate system (i.e., a graph). If the first point is (x1, y1) and the second point is (x2, y2), then the distance formula is:
This formula, by itself, just seems arbitrary. Why would this particular formula give you the distance between points? Who says that it is right? Did this math just drop out of the sky? When students feel like they are memorizing arbitrary scribbles on a page, many of them start to check out. Our goal as parents is to keep them connected to the material.
While the development of this formula is somewhat explained in Saxon Algebra 2, the explanation is brief, and most students I have encountered don’t understand/remember where the formula comes from.
The interesting thing is that understanding where this formula comes from is probably more important than the formula itself:
- Understanding where the formula comes from means that students can easily recreate the formula if they forget it.
- Understanding how ideas are connected is important, as it will enable students to see how they can use similar techniques to develop new ideas when they need them.
- Understanding that all of the ideas are related to each other helps students get excited about learning. They can more easily see the whole conversation they are entering into, rather than fragmented pieces.
Help from The Pythagorean Theorem
Let’s take a brief digression to discuss the Pythagorean Theorem. (I promise you, this will wind up being relevant to our discussion, and soon you’ll understand how the pythagorean theorem is related to the distance formula.)
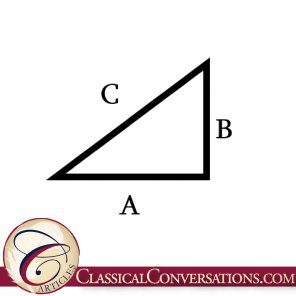
One of the easiest formulas in mathematics to memorize is the Pythagorean Theorem. The Pythagorean Theorem starts with a right triangle with sides of length A and B, with a hypotenuse of length C.
The Pythagorean Theorem states that the lengths of the sides are related by this simple formula:
So, if I have a triangle with sides of length 3 and 4, then I can apply this formula to find the length of the hypotenuse. First, I plug in 3 and 4 into A and B of the equation. This gives me:
Or, to simplify, we can say that:
So, to find C, we just take the square root of both sides:
So, we have used the basic rules of algebra to find the length of the hypotenuse given sides A and B.
Now, let’s say that we didn’t want to use algebra to find the length of the hypotenuse. That is, we wanted a formula which was solved for C, so we didn’t have to solve for C each time. In other words, we want to manipulate the Pythagorean Theorem ahead of time to solve for C, rather than doing it after we plug in our numbers each time.
Interestingly, the same rules of algebra we use afterwards also apply before we plug in our numbers. For instance, we can do anything we want to our equation, as long as we do the same thing to both sides. Therefore, since we want C to wind up on a side by itself, but right now C-squared is on a side by itself, we can solve for C by simply taking the square root of both sides of the Pythagorean Theorem. This will give the following equation, which is identical to the Pythagorean Theorem, but solved for C:
Okay, that’s nice. But what how is the Pythagorean Theorem related to the distance formula?
How is the Pythagorean Theorem Related to the Distance Formula?
It turns out that our reworked Pythagorean Theorem actually is the exact same formula as the distance formula. I will show why shortly. However, for now, I just want you to take a look at the symmetry between what we have developed so far and the distance formula as is given in the book:
Note that in both cases, the final outcome is the result of square-rooting the sum of two squared items. It may not be clear yet why these formulas are related, but I think it is helpful at this point just to see that there is a clear connection in the way that these formulas are structured.
So, why are these formulas so similar? To see why, let’s take our right triangle and stick it on a sheet of graph paper.
Notice the two dots that I put on the triangle. Remember, in the distance formula, we were trying to go between two points on a graph. These dots represent the two points. The hypotenuse of the triangle, C, is overlaid so that it makes a straight line between these two points. This means that the distance between the two points will be the same as the hypotenuse of the triangle.
Now, notice that, on graph paper, you can always make a right triangle by taking the line between two points as a hypotenuse, and then using the x and y parts of the graph as your A and B. Since the triangle in this case starts at the origin (the center of the graph), A is the same as the x value on the graph, and B is the same as the y value on the graph. This means that we can replace A and B in the Pythagorean Theorem with x and y, and replace the hypotenuse, C, with the distance, D. Therefore, our equation becomes:
This is almost the same as the distance formula, but not quite. Why is our formula different?
Well, this formula assumes that the first point starts at the origin. The distance formula can be used for any two points on the graph. So, let’s move our triangle around, and see how this affects the formula.
Now, the distance hasn’t change, but our starting point has. In this case, the first point is at (1, 2) and the second point is at (5, 5). However, even though the graph has changed, the concept has not changed. The A still represents a traveling distance along the x axis. However, since we aren’t at the origin, we have to subtract our starting and ending x to get A. So, we can say that the length A is just x2 – x1. Likewise for B. B is the traveling distance along the y axis. Therefore, B is just y2 – y1.
So, if we plugin x2 – x1 for A, and y2 – y1 for B, we will get this:
And that is the distance formula!
The Journey, Not the Destination
I find the most important thing in explaining the distance formula to students is making sure they see how the Pythagorean Theorem is related to the distance formula. Seeing how these two concepts are related helps them as students to see the world as full of understandable connections rather than a collection of arbitrary facts. It helps them to imagine how they might one day be able to participate in this great journey of knowledge rather than be a passive recipient of it. It enables them to probe deeper into any subject, as it will give them a foundational trust that knowledge is both related and knowable, and therefore they will have the automated desire to understand connections in the future, and even to search them out and identify such connections themselves.
Additionally, seeing connections like this will also help students to judge knowledge given to them in the future, because they will have a sense of where knowledge comes from. They will know that facts do not appear magically from the sky, but are discovered based on previously known facts and basic problem-solving. This will prevent them from being deceived by false claims of knowledge in the future.
In short, it is important in mathematics to realize that the equations themselves are not always the most important part. The most important part is the ability to reason about the equations, and to see the logical relationships between them. You may never have to use the distance formula in your life, but you will have to use part of your brain that connects ideas in the same way that the Pythagorean Theorem is related to the distance formula. Having practice with concrete ideas such as these will help your students to connect more abstract ideas in the future.
Whether you’re interested in homeschooling, the Classical Conversations programs and curriculum, or our community-based, Christ-centered approach to education, we’d love to hear from you. Click here to learn more!